DEFINICIÒN
La serie de Taylor de una función f de números reales o complejos que es infinitamente diferenciable en un entorno de números reales o complejos a, es la serie de potencias:
que puede ser escrito de una manera más compacta como

donde n! es el factorial de n y f (n)(a) denota la n-ésima derivada de f en el punto a; la derivada cero de f es definida como la propia f y (x − a)0 y 0! son ambos definidos como uno.
Si esta serie converge para todo x perteneciente al intervalo (a-r, a+r) y la suma es igual a f(x), entonces la función f(x) se llama analítica. Para comprobar si la serie converge a f(x), se suele utilizar una estimación del resto del teorema de Taylor. Una función es analítica si y solo si se puede representar con una serie de potencias; los coeficientes de esa serie son necesariamente los determinados en la fórmula de la serie de Taylor.
A continuación se enumeran algunas series de Taylor de funciones básicas. Todos los desarrollos son también válidos para valores complejos de x.
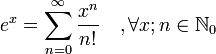
Los números Bk que aparecen en los desarrollos de tan(x) y tanh(x) son Números de Bernoulli. Los valores C(α,n) del desarrollo del binomio son los coeficientes binomiales. Los Ek del desarrollo de sec(x) son Números de Euler.
Varias variables
La serie de Taylor se puede generalizar a funciones de d variables:
donde  es un coeficiente multinomial. Como ejemplo, para una función de 2 variables, x e y, la serie de Taylor de segundo orden en un entorno del punto (a, b) es:
es un coeficiente multinomial. Como ejemplo, para una función de 2 variables, x e y, la serie de Taylor de segundo orden en un entorno del punto (a, b) es:
 es un coeficiente multinomial. Como ejemplo, para una función de 2 variables, x e y, la serie de Taylor de segundo orden en un entorno del punto (a, b) es:
es un coeficiente multinomial. Como ejemplo, para una función de 2 variables, x e y, la serie de Taylor de segundo orden en un entorno del punto (a, b) es:Un polinomio de Taylor de segundo grado puede ser escrito de manera compacta así:

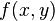
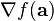 es el
es el 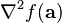 es la
es la 

No hay comentarios:
Publicar un comentario