SERIE DE POTENCIA
Series De Potencia Series de potencias Convergencia de las series de potencias Definición Recibe el nombre de serie de potencias toda serie de la forma ∞Σ n=0 an(x−c)n. El número real an se denomina coeficiente n-ésimo de la serie de potencias (obsérvese que el término n-ésimo de la serie es an(x−c)n). Si los coeficientes a0, a1, am−1 son nulos, la serie suele escribirse ∞Σ n=m an(x−c)n. En cierto modo, se trata de una especie de polinomio con infinitos términos. Vamos a ver que las funciones definidas como suma de una serie de potencias comparten muchas propiedades con los polinomios. ¿Para qué valores de x converge una serie de potencias? Obviamente, es segura la convergencia para x =c, con suma a0, y puede suceder que éste sea el único punto en el que la serie converge. Fuera de este caso extremo, la situación es bastante satisfactoria: veamos algunos ejemplos. Ejemplos. a) La serie geométrica ∞Σ n=0 xn converge (absolutamente) si y solo si x “ (−1,1) (con suma 11−x , como sabemos). 189
DEFINICION
Una serie de potencias alrededor de x=0 es una serie de la forma:
Una serie de potencias alrededor de x=c es una serie de la forma:
En el cual el centro es c, y los coeficientes an son los términos de una sucesion.
EJEMPLOS
- La serie geométrica
 es una serie de potencias absolutamente convergente si | x | < 1 y divergente si | x | > 1 ó | x | = 1
es una serie de potencias absolutamente convergente si | x | < 1 y divergente si | x | > 1 ó | x | = 1
- La serie de potencias
 es absolutamente convergente para todo
es absolutamente convergente para todo 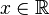
- La serie de potencias
 solamente converge para x = 0
solamente converge para x = 0
BIBLIOGRAFIA:

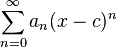
No hay comentarios:
Publicar un comentario